Equações de Maxwell

As equações de Maxwell formam um grupo de quatro equações que juntas descrevem as relações entre eletricidade e magnetismo. Elas são assim:

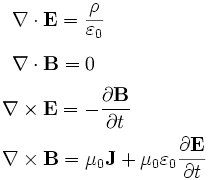
Esta notação matemática envolve cálculo vetorial. Mas relaxe, todos podem entender as equações de Maxwell, sua importância e beleza, se as explicamos bem claramente. Vamos lá.

James Clerk Maxwell foi um físico escocês que viveu em meados do século 19. Ele se interessou pelas então novas ciências da eletricidade e magnetismo, e as intrigantes pistas de que as duas eram de alguma maneira relacionadas – pistas que surgiram do trabalho de cientistas anteriores como Hans Christian Ørsted, Michael Faraday e André-Marie Ampère. Ørsted descobriu em 1820 que a agulha magnética de uma bússola deixava de apontar o norte para apontar em outra direção quando um circuito elétrico próximo, alimentado por uma bateria, era ligado. Esta observação causou uma completa surpresa, pois até então ninguém suspeitava que a eletricidade tinha algo a ver com o magnetismo.

Ampère logo ouviu sobre a descoberta de Ørsted, e em apenas uma semana formulou uma teoria matemática para descrevê-la. Ele postulou que uma corrente elétrica podia gerar um campo magnético, e que ligar ou desligar esta corrente significava alterar o campo magnético (de não estar ali, para estar, ou vice-versa). Esta mudança no campo magnético afetava a agulha da bússola. Faraday, enquanto isso, trabalhava na idéia oposta: que um campo magnético em movimento (ou oscilando) podia fazer surgir uma corrente elétrica num fio. Ele provou sua teoria e a usou para inventar o dínamo elétrico, um gerador de eletricidade similar em essência aos utilizados hoje em dia nas usinas de força. Repare como tudo isto é importante, e nós nem chegamos a Maxwell ainda!

Maxwell formalizou e estendeu o trabalho de Ampère e Faraday, combinando suas descobertas num conjunto interligado de equações que descreve completamente todos os aspectos da eletricidade e do magnetismo como eram então entendidos. As equações de Maxwell ainda formam a base da teoria do eletromagnetismo, tal como aprenderam gerações de estudantes de física, e sustentam tudo que sabemos e fazemos envolvendo eletromagnetismo.

Equação Um

A primeira equação diz que “a divergência do campo elétrico é igual à densidade da carga dividida por ε_o." Certo, mas o que isso significa? O ε_o (a letra grega epsilon com um zero subscrito) é apenas um número; vamos vê-lo num minuto. Campo Elétrico, em termos gerais, é uma medida de quanta influência elétrica existe em um lugar. Já esteve numa feira de ciências e colocou a mão naqueles geradores eletrostáticos que fazem seu cabelo ficar em pé ? Então sabe como sentimos um campo elétrico. (Neste texto evitaremos as definições científicas precisas em favor de um melhor entendimento da história da ciência, certo?)

Divergência é uma medida matemática de quanto de algo vem de algum lugar. Por exemplo: quando abrimos uma torneira a água aparece. Matemáticamente, a divergência de água na abertura da torneira é um número positivo. A divergência de água no ralo da pia onde ela desaparece é um número negativo. Portanto, se não retiramos água do sistema para encher um copo por exemplo, a divergência em todo o conjunto (torneira e ralo somados) é zero, o que significa que sai pelo ralo exatamente a mesma quantidade de água que é adicionada pela torneira.

Assim, a divergência (aquele triângulo e o ponto na equação) do campo elétrico (a letra E) é quanto campo elétrico vem de algum lugar. Isto é igual à densidade da carga elétrica (a letra grega ρ, "rho") no mesmo lugar, dividida por aquele número ε_o. Está bem, agora sabemos o que diz a equação, mas o que isto na verdade significa?

A quantidade de campo elétrico vindo de uma região do espaço é igual à carga elétrica nesta região do espaço (dividida por um número).

Carga elétrica é uma propriedade de partículas subatômicas, como elétrons e prótons. Elétrons têm carga negativa, enquanto prótons têm carga positiva. Se numa região do espaço existem mais prótons que elétrons, a carga total é positiva, e o campo elétrico ali é positivo. Prótons são como torneiras para o campo elétrico. Por outro lado, elétrons são como ralos para o campo elétrico. Se uma região do espaço tem mais elétrons do que prótons, a carga total é negativa, e o campo elétrico nesta região é negativo.

* A ciência é cheia de analogias espertas. As mais divertidas são quando comparamos (digamos um campo elétrico) com algo parecido (um fluxo de água), a não ser pelo fato que alguma propriedade importante dele (que a água se move) simplesmente não existe no primeiro. ** Sim, volts por metro. Se pegamos dois fios, um aterrado e outro com 100 volts, e os separamos por um metro de distancia, geramos um campo elétrico de 100 volts por metro entre eles.

Assim podemos pensar no campo elétrico como um fluxo de água, exceto que na verdade nada se move*. Entretanto, se colocarmos uma carga elétrica, por exemplo um próton, num campo elétrico, ele será levado pelo campo, afastando-se de áreas de carga positiva e em direção a áreas de carga negativa. Um elétron, tendo uma carga negativa, fará o caminho inverso. Isto explica algo já aprendido na escola: que coisas com cargas elétricas iguais se repelem enquanto coisas com cargas elétricas opostas se atraem.

Agora, e aquele ε_o pendente? Este número é chamado a permissividade do espaço livre. É uma constante, e seu valor depende das unidades usadas para descrever carga elétrica e campo elétrico. Físicos geralmente medem carga elétrica em coulombs, e campo elétrico em volts por metro**.

Nestas unidades, ε_o assume o valor aproximado 0.0000000000088541878176. Lembre dele.

Equação Dois

A segunda equação de Maxwell agora ficou fácil. A única novidade é a letra B representando o campo magnético. Por que B e não M? Não sei, ficou assim. Agora podemos ler a equação sozinhos. O triângulo e o ponto dizem “divergência” como na equação um.

Assim esta equação fica: “a divergência do campo magnético é zero”. Fácil!

E o que isso realmente significa?

Significa que para campos magnéticos não existem coisas como torneiras e ralos. Campos magnéticos não vêm de algum lugar nem vão para algum lugar. Mas certamente existem. Como isto é possível?

Campos magnéticos “fluem” dos polos norte magnéticos aos polos sul magnéticos (da mesma maneira que os campos elétricos “fluem” dos prótons para os elétrons, embora nada se mova.) Mas magnetos sempre apresentam os dois polos, o norte e o sul. Se cortarmos um magneto pela metade, não teremos apenas o polo norte e um polo sul separado, e sim faremos dois magnetos menores, cada um com polo norte e polo sul.

Campos magnéticos não vêm do polo norte e vão para o polo sul. O que acontece é que o campo magnético sai do magneto pelo polo norte, flui através do espaço até o polo sul, volta ao magneto, e flui através do interior do magneto até o polo norte, de onde sai novamente. Campos magnéticos existem como um laço contínuo, nunca começando e nunca terminando. É por isso que ao cortarmos um magneto ao meio não separamos o polo norte do polo sul. A metade com o polo norte original ainda terá o polo norte no mesmo ponto de onde sai o campo magnético, mas este tem de retornar ao magneto pela outra ponta, no polo sul.

Em poucas palavras, polos magnéticos sozinhos - ou monopolos magnéticos – não existem. Um monopolo magnético seria o equivalente magnético de um elétron ou próton – uma partícula que originaria um campo magnético onde estivesse.

Na verdade não há uma forte razão teórica pela qual os monopolos magnéticos não possam existir. Apenas parece que é assim. Nunca vimos um, embora os cientistas procurem há muito tempo. Se eles aparecerem não haverá um desastre. Tudo que temos que fazer é adicionar uma “densidade de carga magnética” à segunda equação de Maxwell, no lugar do zero, analogamente à densidade de carga elétrica da equação um. Monopolos magnéticos são portanto bons candidatos a “partículas exóticas” na ficção científica.

Equação Três

Vamos à equação três, que afirma que “a curvatura do campo elétrico é (menos) a taxa de variação do campo magnético”. Do lado esquerdo E é o nosso velho amigo o campo elétrico. O triângulo e o símbolo de cruzamento representam a operação matemática conhecida como “curvatura”, que é bem o que o nome diz. A curvatura do campo elétrico é uma medida de quão “curvo” ele é, de quanto ele se torce em volta do eixo, formando círculos.

Na nossa analogia com um fluxo dágua, em um rio, a maior parte da água segue em frente pela sua calha. Em alguns pontos, entretanto, a água volteia em redemoinhos. Nesses pontos a curvatura da água é diferente de zero.

A curvatura do campo elétrico é igual a (menos) a taxa de variação do campo magnético. (os símbolos ∂ e o t embaixo significam “taxa de variação”.) Taxa de Variação é exatamente o que parece: quão rápido o campo magnético muda. Se o campo magnético não muda, então a taxa de variação é zero, e o campo elétrico é não-curvo. Se o campo magnético muda, então o campo elétrico se curva. Se o campo magnético enfraquece, a taxa de variação é negativa, e a curvatura do campo elétrico é positiva. Se o campo magnético fica mais forte, a taxa de variação é positiva, e a curvatura do campo elétrico é negativa - quer dizer, ele se curva em direção oposta.

Como um campo magnético fica mais forte ou mais fraco? Imagine um campo magnético em algum ponto no espaço. Se ali o campo magnético é zero, e trazemos para perto um magneto, o campo magnético fica mais forte. Se o afastamos, o campo fica mais fraco. Basicamente, se agitamos magnetos, geramos um campo magnético oscilante, que por sua vez gera curvatura no campo elétrico. Mas o que é um campo elétrico curvo?

A curvatura no campo elétrico empurra as cargas elétricas em círculos.

E também:

Cargas elétricas em círculo formam uma corrente elétrica.

Juntando tudo...

Oscila. Magnetos. Em volta. Gera. Corrente. Elétrica.

Esta é a base da revolucionária invenção de Faraday: o gerador elétrico. Ele entendeu que se tomamos alguns fios, e agitamos magnetos próximo deles, geramos eletricidade. Se usamos por exemplo uma máquina a vapor, ou uma roda dágua para mover os magnetos para nós, então temos uma usina elétrica a carvão ou uma moderna usina hidroelétrica. Sem James Clerk Maxwell, seus predecessores, e suas equações, nossas vidas seriam muito, muito diferentes.

A última equação...

Equação Quatro

Agora conseguimos ler quase tudo da equação quatro sozinhos. “a curvatura do campo magnético é igual a μ_o vezes a letra J, mais μ_o vezes ε_o vezes a taxa de variação do campo elétrico.” Correto! O novo termo J se refere à densidade da corrente, que explicaremos num minuto. Esta equação é um pouco maior, então vamos vê-la por partes.

Comecemos pela curvatura do campo magnético. Quão curvo é um campo magnético? Bem, vimos que um campo magnético sempre forma um laço contínuo, do polo norte ao polo sul e de volta ao polo norte por dentro do magneto. Sim, significa que é sempre curvo. Quanto mais forte o campo, mais apertado é o laço – e mais curvo ele é. De fato, a curvatura de um campo magnético é a própria medida de sua força.

Assim a curvatura (ou força) de um campo magnético é igual a μ_o vezes a densidade da corrente (mais a outra parte, que veremos a seguir). Densidade da corrente é quanta corrente elétrica está presente em algum lugar. O que esta parte da equação diz é que onde há uma corrente elétrica, há sempre um campo magnético curvo à sua volta.

*** O que acontece quando ligamos um aparelho? Súbitamente mudamos de corrente elétrica nenhuma para alguma corrente elétrica. Significa que antes não havia nenhum campo magnético e que agora há, tornando-se mais forte. Lembra-se da equação três? Um campo magnético oscilante gera uma corrente elétrica...Esta é a fonte potencial de interferência entre os aparelhos elétricos. É por isso que usar o liquidificador faz a televisão ficar ruim. E é por isso que o computador tem cabos blindados, para evitar que qualquer campo magnético oscilante na área estrague os dados.

Imagine um fio levando corrente elétrica. Segure-o com a mão. Seus dedos estão curvos sobre o fio da mesma forma que o campo magnético se curva em torno dele. É assim que funcionam os eletromagnetos. Eles têm muitos fios, e quando uma corrente elétrica passa por eles, eles geram um campo magnético. Toda a fiação ativa numa casa gera campos magnéticos também, embora estes sejam relativamente fracos***.

De novo, assim como o ε_o, o termo μ_o (letra grega mu com um zero subscrito) é apenas um número constante que faz as unidades de medida aparecerem da forma correta. É chamado permeabilidade do espaço.

Quando o campo magnético é medido em teslas e a densidade da corrente em amperes por metro quadrado, μ_o é igual a 0.000001256637061. Lembre-se deste número também.

Repare que esta equação é para o campo magnético o que a equação um é para o campo elétrico. A equação um diz que o campo elétrico total depende da carga elétrica total. A equação quatro diz que o campo magnético total depende da corrente elétrica total. Interessante...

Agora, e sobre aquele termo extra: "μ_o vezes ε_o vezes a taxa de oscilação do campo elétrico"? Não é difícil entender. Se há um campo elétrico que fica mais forte ou mais fraco, ele gera um campo magnético. Fácil!

Esta última parte é a maior conquista de Maxwell, sua gloriosa coroação, seu profundo e duradouro acréscimo ao nosso entendimento do universo. Ela diz que para gerar um campo magnético, nem mesmo precisamos de uma corrente elétrica. Basta um campo elétrico oscilante.

Vejamos as implicações disto.

Um campo elétrico oscilante gera um campo magnético. Imagine um campo elétrico que se altere, indo para frente e para trás, do positivo para o negativo. Além disso, como a taxa de oscilação do campo elétrico precisa mudar, de maneira a permitir que o campo oscile para frente e para trás, o campo magnético não será constante e mudará com o tempo.

Mas lembre-se, a equação três nos diz: um campo magnético que oscila gera um campo elétrico.

O campo magnético oscilante gera um campo elétrico oscilante. Este gera um campo magnético oscilante. Que gera um campo elétrico oscilante...

Com as equações três e quatro podemos fazer alguns cálculos assumindo que a densidade da corrente J é zero (isto é, não há corrente elétrica). Sem detalhar a álgebra, as equações ficam:

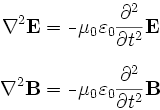
Como podemos ver, elas são idênticas, exceto que uma se refere apenas ao campo elétrico enquanto a outra se refere apenas ao campo magnético. Em essência, o que elas nos dizem é que um campo elétrico que varia com o tempo (na direita) gera um campo elétrico que varia no espaço (na esquerda) de uma maneira precisamente determinada, e que o mesmo vale para o campo magnético. De fato, estas duas equações descrevem o movimento de propagação dos campos elétrico e magnético, que viajam pelo espaço como ondas.

Conhecendo cálculo diferencial, podemos resolver estas equações para chegar à velocidade de propagação destas ondas, velocidade que acaba dependendo daqueles números ε_o e μ_o e que é:

Imagine que você é James Clerk Maxwell, in 1865, formulando sua teoria da eletricidade e magnetismo, e escrevendo suas quatro equações pela primeira vez na história. Você escreve os termos destas equações com base nos seus experimentos com baterias elétricas, pedaços de fio e magnetos. Percebe que precisa definir algumas constantes (ε_o and μ_o) para que os valores previstos sejam corretos. Mede os valores destas constantes... Os números não parecem com nada na hora - são apenas algum tipo de constante que a natureza parece usar. Afinal poderiam ter qualquer valor, pelo que você sabe. De qualquer modo, você os coloca no papel.

Você nota que com alguma álgebra nas suas novas equações, aparecem uma equação que se refere apenas ao campo elétrico, e uma quase idêntica que se refere ao campo magnético. Ao resolvê-las percebe que elas descrevem a propagação em ondas dos campos elétrico e magnético. Calcula a velocidade das ondas e nota que ela depende daqueles valores que você mediu para ε_o e μ_o.

Aí faz a aritmética. Pega as medições para ε_o e μ_o, multiplica um pelo outro, extrai a raiz quadrada e toma a recíproca. A resposta é uma velocidade, portanto com unidades de velocidade, neste caso metros por segundo. E a resposta é muito próxima a 300.000.000 metros por segundo. Sendo James Clerk Maxwell, e um físico brilhante, você imediatamente reconhece o que é aquele número.

A velocidade da luz.

De onde ele veio?

Você sabe em 1865 pelo trabalho de Isaac Newton e outros que a luz tem certas propriedades: que a luz branca é composta de múltiplas côres de luz misturadas juntas; que materiais transparentes como vidro desviam os raios de luz e podem ser usados para focalizá-los em imagens, como nos telescópios; e que a luz difrata quando passa por pequenos orifícios ou fendas estreitas. Esta propriedade de difração somente se explica pela suposição de que a luz é feita de algum tipo de onda. Mas ninguém no mundo sabe qual tipo de onda. Ninguém sabe o que a luz na verdade é.

Ninguém no mundo - exceto você - sabe o que a luz é realmente.

Enquanto escrevia suas equações, pensava sobre eletricidade e magnetismo. A luz era a coisa mais distante de sua mente. Você não tinha a menor pista (e nem mais ninguém) de que a luz era relacionada com eletricidade e magnetismo. Mas ali estava, surgindo de suas equações.

Você se dá conta que é a primeira pessoa em toda a história a saber do que a luz é feita. Pode imaginar esta emoção?

As equações de Maxwell deram à humanidade, finalmente, uma compreensão do que a luz realmente é. Sua descoberta foi impressionante e revolucionária. Luz é feita de campos elétricos e magnéticos movendo-se juntos pelo espaço.

Desta revolução surgiram incontáveis outras descobertas sobre a natureza da luz, assim como de suas irmãs as ondas eletromagnéticas: rádio, microondas, infravermelho e ultravioleta, raios x, e raios gamma. Todas estas formas de radiação são feitas de campos elétricos e magnéticos, movendo-se pelo espaço à velocidade da luz, exatamente como descrito pelas equações de Maxwell. Hoje sabemos que ondas de rádio, por exemplo, podem ser geradas pelo chaveamento muito rápido de uma corrente elétrica. Os elétrons nos fios oscilando para frente e para trás, criando campos elétricos oscilantes, que criam campos magnéticos, e assim por diante - o efeito total sendo as ondas de rádio. E ondas de rádio por sua vez agitam os elétrons na antena de seu rádio ou TV, criando correntes elétricas que os vários circuitos eletrônicos transformam de novo em som e imagem.

Muitas tecnologias que usamos todo dia revelam o nosso conhecimento de eletromagnetismo e suas interações com a luz. A civilização como a conhecemos simplesmente não existiria sem James Clerk Maxwell e suas quatro equações. Esperamos ter-lhe mostrado como elas são realmente geniais.

Irregular Webcomic!

Copyright © 2002-2008, David Morgan-Mar. dmm@irregularwebcomic.net Hosted by: DreamHost

Tradução: Marcos Pereira de Sousa.

NOTA do TRADUTOR: Os LINKS deste texto foram mantidos como no original.